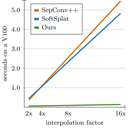
| Revisiting Adaptive Convolutions for Video Frame Interpolation Simon Niklaus, Long Mai, and Oliver Wang We show, somewhat surprisingly, that it is possible to achieve near state-of-the-art frame interpolation results with an older and simpler approach, namely adaptive separable convolutions, through a subtle set of low level improvements. |
 | Learned Dual-View Reflection Removal S. Niklaus, X. Zhang, J. T. Barron, N. Wadhwa, R. Garg, F. Liu, and T. Xue Typical dereflection algorithms either use a single input image, which suffers from intrinsic ambiguities, or use multiple images from a moving camera, which is inconvenient. We instead propose an algorithm that uses stereo images as input. |